दशकों से गणितज्ञों को परेशान करने वाली कुख्यात 'सोफा समस्या' का आखिरकार समाधान हो सकता है

रॉस को अपने अपार्टमेंट में नया सोफ़ा लाने में मदद करने के लिए पच्चीस साल बहुत देर हो चुकी है “दोस्त,” एक गणितज्ञ ने आख़िरकार कष्टप्रद “सोफ़ा समस्या” को हल कर लिया है।
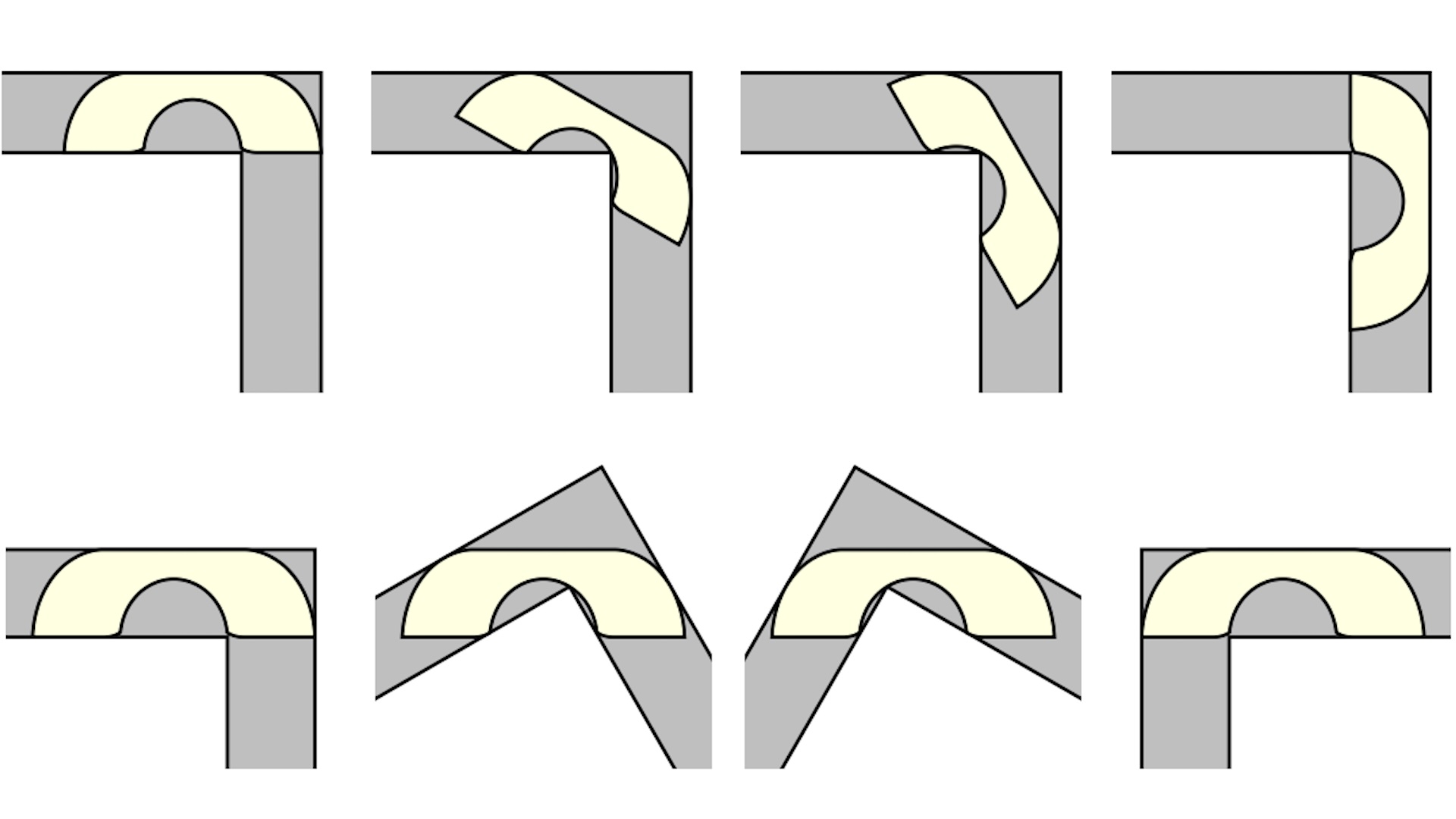
गणित की समस्या सबसे बड़े आकार के सोफे को चित्रित करती है जो दी गई चौड़ाई के एक कोने के चारों ओर फिट हो सकता है – बिल्कुल वही समस्या जिसका सामना 1999 में प्रसारित “फ्रेंड्स” के एक एपिसोड में पात्रों ने किया था। रॉस की “पिवोट!” की दलील! इससे बचा जा सकता था, यह पता चला है, अगर उसने केवल 18 वक्र खंडों और 2.2195 इकाइयों के अधिकतम क्षेत्रफल वाले गेरवर सोफे पर विचार किया होता। (ठीक है, तो शायद यह उतना मददगार नहीं होता।)
सोफे की समस्या का समाधान गणित के लिए सबसे पहले है। समस्या 1966 में ऑस्ट्रियाई-कनाडाई गणितज्ञ लियो मोजर द्वारा प्रस्तुत की गई थी। मोजर ने एक विमान में एक ही आकार के सबसे बड़े संभावित क्षेत्र के लिए कहा था जो एक इकाई चौड़ाई के साथ दालान के समकोण कोने के चारों ओर घूम सकता था। हालांकि यह सरल लग सकता है, गणित काफी जटिल है, क्योंकि समस्या में क्षेत्र अधिकतमकरण और आकृति की गति दोनों शामिल हैं।
अब, जिनेओन बाकदक्षिण कोरिया में योनसेई विश्वविद्यालय में गणित में पोस्टडॉक्टरल शोधकर्ता, एक उत्तर पर पहुंचे हैं। बेक ने अपना समाधान 2 दिसंबर को प्रीप्रिंट वेबसाइट पर पोस्ट किया arXiv. गणितीय प्रमाणों के केवल 100 से अधिक पृष्ठों में, बाक ने पाया कि 1 इकाई की चौड़ाई वाले दालान के लिए, काल्पनिक सोफे का अधिकतम क्षेत्र 2.2195 इकाई हो सकता है – 2.2195 और 2.37 इकाइयों के बीच की पहले से ज्ञात सीमा से सटीकता के साथ उत्तर को कम करना। प्रमाण अभी तक किसी सहकर्मी-समीक्षित पत्रिका में प्रकाशित नहीं हुआ है और यह निर्धारित करने के लिए कि यह वास्तव में इष्टतम है, अन्य गणितज्ञों द्वारा इस पर काम करने की आवश्यकता होगी।
संबंधित: पाइथागोरस प्रमेय के 'असंभव' प्रमाण के साथ आए हाई स्कूल के छात्रों ने समस्या के 9 और समाधान खोजे
गेरवर के सोफे के “गर्वर” गणितज्ञ जोसेफ गेरवर हैं, जो रटगर्स विश्वविद्यालय के एक एमेरिटस प्रोफेसर हैं। 2.2195 की निचली सीमा निर्धारित की 1992 में। लेकिन इस बात पर बहस चल रही थी कि क्या सोफा बड़ा हो सकता है, 2018 में एक टीम ने कंप्यूटर-समर्थित प्रमाण का उपयोग करके यह सुझाव दिया था 2.37 वास्तव में ऊपरी सीमा थी.
गेरवर का सोफ़ा एक घुमावदार “सीट” वाला एक चौड़ा यू-आकार का सोफ़ा है जो बिना लटके कोने के चारों ओर घूम सकता है। सवाल यह था कि क्या बड़ी मेहनत से डिजाइन किया गया यह सोफा – जो 18 अलग-अलग घुमावों को एक साथ जोड़कर बनाया गया था – वास्तव में सबसे बड़ा, सबसे इष्टतम आकार था जो मोड़ बना सकता था। बेक ने आकृति की ज्यामिति और उसकी गति पर काम किया और पाया कि गेवर का समाधान वास्तव में सही था।
इस सबूत ने सोशल मीडिया पर दिलचस्पी की लहर पैदा कर दी।
उपयोगकर्ता ने कहा, ''यह सबसे अच्छा सोफा है।'' @morallawwithin 6 दिसंबर को सोशल प्लेटफॉर्म एक्स पर चौड़े भुजाओं वाले सोफे के आकार की एक तस्वीर पोस्ट करते हुए लिखा। “हो सकता है आपको यह पसंद न आए, लेकिन शिखर अनुकूलन ऐसा ही दिखता है।”



